Interpretación Física y Geométrica de la Derivada.
Vector Tangente, Vector Normal y Vector Binormal
La tangente de una curva es una recta que intersecta la curva en un solo punto. Es conocido por nosotros a través del cálculo que mediante la diferenciación de una función se obtiene el punto tangencial para la curva de esa función. Un concepto similar es aplicable al cálculo vectorial, junto con una excepción.
Para una función con un vector de la forma, (x), un vector de la forma es llamado vector tangente en el caso de que esta función sea real y su magnitud no sea igual a cero. En esta situación, la tangente de la función dada (x) en un punto arbitrario es paralela al vector tangente, en ese punto. Aquí, con el fin de tener un vector tangente, 0 es un pre-requisito esencial. Esto es debido a que un vector de magnitud cero no puede tener dirección.
De manera similar, un vector tangencial unitario es definido como,



Aquí s es la longitud total del arco dado, (t) es el vector posición de la función dada y t es la variable de parametrización.

En la figura anterior, X es un punto estático, mientras que P es un punto en movimiento. El punto P se mueve lentamente en la dirección del punto X, mientras el punto P se acerca al punto X, el vector desde el punto X hasta el punto P se acerca al vector tangente en el punto X. La recta que contiene el vector tangente se conoce como recta tangencial.
Un vector normal es algo similar a un vector unitario, suponga que para una función (x), (t) es el vector posición, entonces el vector normal para la función dada es definida como,

Aquí es el vector unitario de la función dada.
Como se describió en la figura anterior, un vector normal es un vector que está perpendicular a un plano o superficie dada. Un vector normal para una superficie dada en un punto arbitrario,sea (x, y), está dado por una matriz como la siguiente,

Aquí fx y fy son diferenciales parciales de la función dada con respecto a x e y.
De la misma forma, el vector normal a un plano es representado por una matriz como,

Donde la ecuación del plano es,
f(x, y, z) = ax + by + cz + d = 0
Un vector binormal es un producto cruz o producto vectorial del vector normal y del vector unitario normal. Suponga que para una función (x), (t) es el vector posición, entonces el vector binormal para la función dada se define como,

Como sabemos que tanto un vector unitario como un vector normal son vectores unitarios y que se encuentran perpendiculares a la superficie dada.
Un vector Binormal es también un vector unitario que se encuentra normal a un plano o superficie dada. Este vector es normal a ambos, el vector unitario y el vector normal.



Curvatura y torsión
La curvatura es una medida del cambio de dirección del vector tangente a una curva, cuanto más rápido cambia éste a medida que nos desplazamos a lo largo de la curva, se dice que es más grande la curvatura. Para una curva parametrizada cualquiera la curvatura es igual a:
Si la curva está parametrizada por el parámetro de longitud de arco, la anterior ecuación se reduce simplemente a:
Además de la curvatura se suele definir el llamado radio de curvatura, como el inverso de la curvatura.
La torsión es una medida del cambio de dirección del vector binormal: cuanto más rápido cambia, más rápido gira el vector binormal alrededor del vector tangente y más retorcida aparece la curva. Por lo tanto, para una curva totalmente contenida en el plano la torsión es nula ya que el vector binormal es constantemente perpendicular al plano que la contiene. Para el caso general la torsión viene dada por:
Si la curva está parametrizada por el parámetro de longitud de arco, la anterior ecuación se reduce a:

Plano Osculador
En cada punto de una curva, el plano osculador es el plano que contiene a su vector tangente y al vector normal a la curva. Para una partícula desplazándose en el espacio tridimensional, el plano osculador coincide con el plano que en cada instante contiene a la aceleración y la velocidad. La ecuación de este plano viene dada por:1 Donde:
Donde: , el punto de la trayectoria.
, el punto de la trayectoria. , el vector velocidad en el punto considerado.
, el vector velocidad en el punto considerado. , las coordenadas de un punto genérico del plano osculador.
, las coordenadas de un punto genérico del plano osculador.
Si se tiene una partícula en la posición , moviéndose con velocidad
, moviéndose con velocidad  y sometida a una aceleración
y sometida a una aceleración  el plano osculador viene dado por el conjunto de puntos:
el plano osculador viene dado por el conjunto de puntos: Obviamente si la partícula tiene un movimiento rectilíneo el plano osculador no está definido.
Obviamente si la partícula tiene un movimiento rectilíneo el plano osculador no está definido.
Radio de curvatura de una curva
El radio de curvatura de una línea curva o un objeto aproximable mediante una curva es una magnitud geométrica que puede definirse en cada punto de la misma y que coincide con el inverso del valor absoluto de la curvatura en cada punto: Por otro lado la curvatura es una medida del cambio que sufre la dirección del vector tangente a una curva cuando nos movemos a lo largo de ésta. Para una curva parametrizada cualquiera la curvatura y el radio de curvatura vienen dados por:1
Por otro lado la curvatura es una medida del cambio que sufre la dirección del vector tangente a una curva cuando nos movemos a lo largo de ésta. Para una curva parametrizada cualquiera la curvatura y el radio de curvatura vienen dados por:1 Si en lugar de un parámetro cualquiera usamos el parámetro de longitud de arco, la anterior ecuación se simplifica mucho, por resultar un vector tangente constante, y puede escribirse como:
Si en lugar de un parámetro cualquiera usamos el parámetro de longitud de arco, la anterior ecuación se simplifica mucho, por resultar un vector tangente constante, y puede escribirse como:
Superficies en Tres Dimensiones.

- Analíticamente la ecuación
 nos representa un lugar geométrico en el plano
nos representa un lugar geométrico en el plano  a la ecuación
a la ecuación  extenderemos al espacio tridimensional, cuya ecuación rectangular en tres variables representadas por:
extenderemos al espacio tridimensional, cuya ecuación rectangular en tres variables representadas por: También se conoce que todo se representa analíticamente por una única ecuación lineal de la forma
También se conoce que todo se representa analíticamente por una única ecuación lineal de la forma De una manera más general, veremos si existe una representación analítica de una figura geométrica, la cual denominaremos superficie, tal representación consistirá en una única ecuación rectangular de la forma:
De una manera más general, veremos si existe una representación analítica de una figura geométrica, la cual denominaremos superficie, tal representación consistirá en una única ecuación rectangular de la forma: Por ejemplo, por medio de la distancia entre dos puntos se puede demostrar que la superficie esférica de radio r con centro en el origen se representa analíticamente por la ecuación.
Por ejemplo, por medio de la distancia entre dos puntos se puede demostrar que la superficie esférica de radio r con centro en el origen se representa analíticamente por la ecuación. La ecuación de la esfera, es solo un caso particular de la ecuación de segundo grado.
La ecuación de la esfera, es solo un caso particular de la ecuación de segundo grado. Cuando
Cuando no son todos nulos, se dice que la gráfica de una ecuación de la forma
no son todos nulos, se dice que la gráfica de una ecuación de la forma es una superficie cuadrática, si describe un lugar geométrico real. Por ejemploEl cilindro elíptico
es una superficie cuadrática, si describe un lugar geométrico real. Por ejemploEl cilindro elíptico Como el cilíndrico parabólico
Como el cilíndrico parabólico Son superficies cuádricas, Concluiremos este informe considerando seis superficies cuádricas adicionales y bien definidas.Se dice que la gráfica de cualquier ecuación de la forma
Son superficies cuádricas, Concluiremos este informe considerando seis superficies cuádricas adicionales y bien definidas.Se dice que la gráfica de cualquier ecuación de la forma
 Es un elipsoide. Para
Es un elipsoide. Para la ecuación
la ecuación Representa una familia de elipses(o circunferencia si a=c) paralelas al plano
Representa una familia de elipses(o circunferencia si a=c) paralelas al plano que se forman cortando la superficie mediante planos
que se forman cortando la superficie mediante planos . Eligiendo, cada uno a su vez
. Eligiendo, cada uno a su vez  , encontrarías que los cortes de la superficie son elipse (o circunferencias) paralelas a los planos
, encontrarías que los cortes de la superficie son elipse (o circunferencias) paralelas a los planos  respectivamente.
respectivamente. HIPERBOLOIDE DE UNA HOJALa gráfica de una ecuación de la forma
HIPERBOLOIDE DE UNA HOJALa gráfica de una ecuación de la forma
 Se llama hiperboloide de una hoja. En este caso, un plano
Se llama hiperboloide de una hoja. En este caso, un plano paralelo al plano
paralelo al plano  corta la superficie en secciones transversales elípticas (o circulares, si a = 0). Las ecuaciones de estas elipses son
corta la superficie en secciones transversales elípticas (o circulares, si a = 0). Las ecuaciones de estas elipses son
 La elipse más pequeña,
La elipse más pequeña, corresponde a las traza en el plano
corresponde a las traza en el plano 
 HIPERBOLOIDE DE DOS HOJASComo se ve en la figura, una grafica de
HIPERBOLOIDE DE DOS HOJASComo se ve en la figura, una grafica de
 Es llamada apropiadamente hiperboloide de dos hojas.Para
Es llamada apropiadamente hiperboloide de dos hojas.Para la ecuación
la ecuación
 Describe la curva elíptica de intersección de la superficie con el plano
Describe la curva elíptica de intersección de la superficie con el plano
 La grafica de una ecuación de la forma
La grafica de una ecuación de la forma Se llama paraboloide. En la Figura vemos que para
Se llama paraboloide. En la Figura vemos que para los planos
los planos paralelos al plano
paralelos al plano  cortan las superficies en elipses cuyas ecuaciones son
cortan las superficies en elipses cuyas ecuaciones son
 Las graficas de una ecuación de la forma
Las graficas de una ecuación de la forma
 Son llamados cono elípticos (o circular, si a=b). Para
Son llamados cono elípticos (o circular, si a=b). Para arbitrario, los planos paralelos al plano
arbitrario, los planos paralelos al plano  cortan la superficie en elipses cuyas ecuaciones son
cortan la superficie en elipses cuyas ecuaciones son En la siguiente figura se muestra una gráfica característica
En la siguiente figura se muestra una gráfica característica La última superficie cuadrática que consideraremos se conoce como paraboloide hiperbólico y es la gráfica de toda ecuación de la forma
La última superficie cuadrática que consideraremos se conoce como paraboloide hiperbólico y es la gráfica de toda ecuación de la forma
 Observe que para
Observe que para los planos
los planos  paralelos al plano
paralelos al plano  cortan la superficie en hipérbolas cuyas ecuaciones son
cortan la superficie en hipérbolas cuyas ecuaciones son En la figura, se muestra la forma característica de la silla de montar de un paraboloide hiperbólico.
En la figura, se muestra la forma característica de la silla de montar de un paraboloide hiperbólico.

- Dominio de Definición.
- En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función
 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 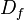 . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina imagen de esa función.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina imagen de esa función. 



No hay comentarios:
Publicar un comentario