Integrales Múltiples
En el caso de funciones constantes, el resultado es trivial: simplemente multiplíquese el valor de la función constante c por la medida del dominio de integración. Si c = 1, y es integrada a través de una región de R2 esto da el área de la región, mientras que si es una región de R3 da el volumen de la región y así sucesivamente.
Por ejemplo:
-
 y
y 
- Integrando f sobre D:
Uso de simetrías
En el caso de un dominio en el que exista simetría al menos respecto de uno de los ejes, y donde la función para integrar contenga al menos una función impar con respecto a esa variable, la integral se vuelve nula (ya que la suma de cantidades iguales con signo opuesto es cero). Por ejemplo
- Dada
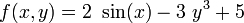 y que
y que 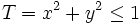 es el dominio de integración del disco de radio 1 centrado en el origen.
es el dominio de integración del disco de radio 1 centrado en el origen.
- Usando la propiedad lineal de las integrales, la integral se descompone en tres partes:
Ya que tanto 2 sin(x) como 3y3 son funciones impares, y existe simetría tanto con respecto al eje x como con respecto al eje y, las primeras dos integrales se nulifican, de tal forma que la integral original es igual únicamente a la tercera.
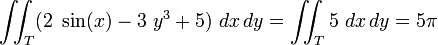
Cambio de variables
A menudo, es útil para reducir la complejidad de la integral cambiar una variable por otra que resulte más cómoda, sin embargo esto exige el cambio de la región de integración, además de añadir un factor de corrección al diferencial conocido como determinante jacobiano (en valor absoluto o módulo). El cambio de una variable por otra es en un sentido geométrico, una transformación desde un espacio hasta otro, y es esta transformación la que exige estos ajustes.
Si se utiliza una transformación que siga la relación:
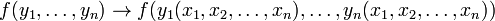
Entonces se puede utilizar el jacobiano de la transformación para simplificar la integral
Integrando la función transformada en el dominio de integración correspondiente a las variables x, y multiplicando por el valor absoluto del determinante jacobiano y por la serie de diferenciales, se obtiene una integral múltiple que es igual a la integral original, si es que esta existe.
A continuación se dan algunos ejemplos de estas transformaciones.
Coordenadas Polares
En un espacio R2, un dominio de integración que tenga una simetría circular es muchas veces suceptible de ser transformado de coordenadas rectangulares a polares, lo que significa que cada punto P (x, y) del dominio de una integral doble tomará su valor correspondiente en coordenadas polares mediante la siguiente transformación:

Por ejemplo:
- Si la función es

- aplicando la transformación se obtiene la función fácilmente integrable con respecto a
 y a
y a  .
.
Se pueden obtener funciones incluso más simples:
- Si la función es

- Uno tiene:
Si aplica la identidad trigonométrica pitagórica de senos y cosenos.
El determinante jacobiano de la transformación es:
El cual se obtiene insertando las derivadas parciales de x = ρ cos(θ), y = ρ sin(θ) en la primera columna con respecto a ρ y en la segunda con respecto a  .
.
 .
.
Por lo tanto, una vez transformada la función, y multiplicada por su determinante jacobiano, ésta es igual a la integral original:
Coordenadas Esféricas
Cuando existe simetría esférica en un dominio en R3, es posible utilizar una transformación hacia coordenadas esféricas para simplificar una integral triple. La función es transformada por la relación:
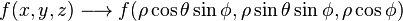
El determinate jacobiano de la transformación es el siguiente:
Tomando el valor absoluto del determinante se obtiene el factor que se debe añadir a la integral.
Por lo tanto los diferenciales dx dy dz se transforman en ρ2 sin(φ) dρ dθ dφ.
Finalmente se obtiene la fórmula de integración:
Coordenadas Cilíndricas
El uso de coordenadas cilíndricas para transformar una integral triple, es conveniente especialmente cuando el dominio de integración presenta simetría alrededor del eje z. La función se transforma mediante la siguiente relación.

El determinate jacobiano de la transformación es el siguiente:
Por lo tanto, se puede derivar la siguiente fórmula de integración:


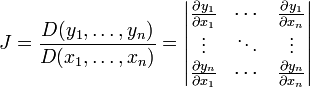


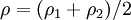 (el radio medio), el área de la región polar es efectivamente
(el radio medio), el área de la región polar es efectivamente  .
.







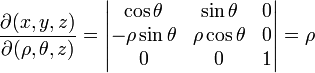

No hay comentarios:
Publicar un comentario